O matemático britânico Professor Ian Stewart apresentou “17 Equações que Mudaram o Mundo”. À medida que entramos no mês de abril para a ciência, gostaríamos de rever brevemente as equações que mudaram o mundo. As quatro equações que serão apresentadas hoje são as equações favoritas dos entusiastas da matemática e da física, e são amplamente utilizadas academicamente.
[9. 푸리에 변환 (Fourier transform: 조제프 푸리에 1822)]
A transformada de Fourier refere-se a uma transformação que decompõe e expressa um sinal de entrada arbitrário em somas de funções periódicas, incluindo as funções trigonométricas de sen e cos de diferentes frequências. O sinal de entrada pode ser uma função do tempo, como um sinal de fala ou uma onda de rádio, ou pode ser uma função do espaço. A razão pela qual a transformada de Fourier mudou o mundo é que ela sempre pode ser decomposta na soma de funções periódicas, independentemente do sinal de entrada. As funções periódicas que compõem o sinal original através da transformada de Fourier possuem frequência e amplitude próprias e, quando todas as funções periódicas são combinadas, elas se tornam iguais ao sinal original.
Transformada de Fourier © sciencetimes
A transformada de Fourier foi concebida pelo matemático francês Joseph Fourier e, embora pareça complicada, é uma transformação bastante simples. Olhando para a fórmula de Euler, que é a “fórmula mais bonita do mundo” que converte uma função exponencial complexa em uma função trigonométrica (abreviatura oficial de Euler) onde a parte real é cos (2πxW), a parte imaginária é -sin (2πxW) é uma função periódica.
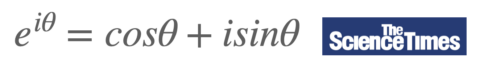
Fórmula de Euler © sciencetimes
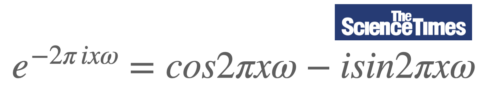
De acordo com a fórmula de Euler, pode-se ver que esta é a mesma função periódica cuja parte real é cos (2πxw) e a parte imaginária é -sin (2πxw). © sciencetimes
Ou seja, ambas as funções periódicas têm um período (o tempo que a onda leva para oscilar) 1/w e a frequência (o número de oscilações por segundo: frequência e período são inversamente relacionados entre si) é w, então a onda senoidal ( no plano coordenado) pode ser visto como uma expressão exponencial complexa de uma curva cíclica aberta – os pontos inicial e final não coincidem. Em conclusão, é o mesmo que dizer que qualquer função complexa pode ser expressa como um conjunto de funções periódicas das frequências possíveis.
A transformada de Fourier é amplamente utilizada nas áreas de comunicação e processamento de imagens de computador. Além disso, é frequentemente usado como solução para equações diferenciais parciais usando propriedades da transformada de Fourier que podem ser decompostas em funções simples e é amplamente utilizado no campo da análise.
[10. 나비에-스토크스 방정식 (Navier-Stokes equation) : 클로드 루이 나비에, 조지 가브리엘 스토크스 1845)]
A equação de Navier-Stokes é uma equação que descreve o movimento de um fluido viscoso. A equação acima é uma equação que expressa a lei da conservação do momento com base nas equações de movimento de Newton (aceleração = força/massa) e nas equações hidrodinâmicas de Euler (equações relativas à conservação de massa, momento e energia de um líquido) para descrever um líquido.
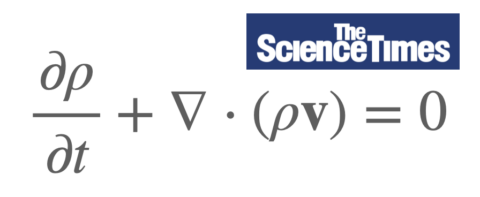
Equação de Euler para conservação hidrodinâmica: ρ é a densidade do fluido e v é a velocidade. © sciencetimes
O lado esquerdo da equação de Navier-Stokes é o termo de aceleração e o lado direito representa a força por unidade de massa que atua no fluido. Ou seja, a aceleração do fluido é determinada pela pressão (p) que atua sobre o fluido, pela resistência (T) gerada no interior quando uma força externa atua sobre o material e pela força (f) distribuída por todo o volume do fluido. fluido em si sem contato físico, uma equação que é determinada pela equação acima é bastante complexa como é, é chamada de uma das equações mais amadas pelos entusiastas da física.
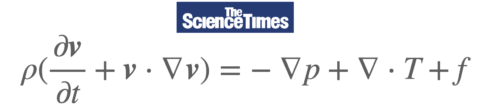
ρ é a densidade do fluido, v é a velocidade, p é a pressão, T é a resistência gerada no interior quando uma força externa atua sobre o material, f é a força distribuída por todo o volume do próprio fluido sem contato físico, ∇ é a inclinação, ∇ representa o espaçamento . © sciencetimes
A equação acima tem a grande vantagem de poder descrever o movimento de um fluido sem coordenadas fixas, e é usada em quase todos os campos da física e da engenharia. Por exemplo, é usado para descrever modelos oceânicos atmosféricos, como modelos climáticos e modelos de correntes oceânicas, o fluxo de sangue em organismos vivos, o fluxo de fluidos em partes de asas de aeronaves e até mesmo em astronomia para explicar o movimento de estrelas ou plasma em galáxias.
[11. 맥스웰 방정식 (Maxwell’s equations) : 제임스 클락 맥스웰 1865)]
A equação de Maxwell é uma das mais amadas por estudantes de ciências naturais e estudantes de engenharia a ponto de não haver necessidade de explicá-la. A equação de Maxwell é uma equação que inclui a lei de Gauss, a lei de Gauss magnética, a lei da indução eletromagnética de Faraday e a lei do circuito de Ampere, a equação mostrou que a luz é uma onda eletromagnética.

Usando a forma diferencial da equação de Maxwell, o teorema da divergência e o teorema de Stokes, a forma integral também pode ser obtida. © sciencetimes
As equações de Maxwell descrevem as propriedades das ondas eletromagnéticas como a luz, em primeiro lugar, a lei de Gauss descreve a força do campo elétrico gerado por uma única carga. A equação acima é frequentemente usada em eletrônica e teoria de circuitos. A segunda lei gaussiana do campo magnético significa que o fluxo magnético total de uma superfície fechada é 0. Devido à propriedade do magnetismo de que não há monopolo e que os pólos N e S estão sempre presentes juntos, a magnitude da linha de campo magnético entrando em um determinado espaço e a linha do campo magnético que sai são sempre as mesmas, então elas são opostas uma à outra, o que significa que a soma das forças que atuam em uma direção é sempre zero. A terceira lei de indução eletromagnética de Faraday é a lei que afirma que, à medida que o fluxo magnético muda, um campo elétrico é criado em torno dele, e esse princípio é usado para gerar corrente alternada em usinas de energia. Finalmente, a lei do circuito de Ampere afirma que um campo magnético é gerado ao longo de um fio através do qual uma corrente elétrica flui. É frequentemente usado em motores elétricos. As equações acima foram criadas uma a uma, pois foram estudadas por um longo tempo, mas não estão organizadas matematicamente. É de grande importância que Maxwell tenha provado matematicamente que eletricidade e magnetismo são uma interação, ou seja, força eletromagnética, combinando os resultados da presente pesquisa. Ele explicou que a luz também é uma onda eletromagnética e previu a descoberta da radiação eletromagnética.

A equação de Maxwell é uma equação comum frequentemente usada como design de camisetas. © www.spreadshirt.at
As equações acima são as equações básicas, mas mais importantes no eletromagnetismo. Além disso, como a mecânica quântica nasceu com base nas equações acima, nem é necessário enfatizar as realizações físicas das equações de Maxwell.
[12. 열역학 제2법칙 (Second law of thermodynamics : 루드비히 볼츠만 1874)]
A lei zero da termodinâmica é uma lei que descreve um estado de equilíbrio térmico.Se dois sistemas termodinâmicos A e B estão em equilíbrio termodinâmico com o outro sistema termodinâmico C, respectivamente, então A e B também estão em equilíbrio térmico. Por outro lado, a primeira lei da termodinâmica é a lei da conservação da energia, que afirma que a energia total de um sistema isolado é constante (o aumento da energia interna). duEnergia térmica adicionada ao sistema de prata BaterO que Ji fez lá fora? Dr.É igual ao valor menosds) para 0, e a entropia no zero absoluto é constante (c) é a regra que

A segunda lei da termodinâmica. S é entropia, Q é calor e T é temperatura. © sciencetimes
Dentre as quatro leis da termodinâmica, por que a segunda lei da termodinâmica mudou o mundo, indicando que a energia de um sistema isolado não aumenta? Em 1824, o engenheiro francês Carnot propôs o “motor de Carnot”, um motor hipotético que poderia alcançar a máxima eficiência de trabalho porque todos os processos são reversíveis. A segunda lei da termodinâmica é uma lei na qual o fluxo de energia flui na direção do aumento da entropia. De acordo com a lei acima, é impossível fabricar um motor permanente que não cause nenhuma mudança externa quando o calor é transferido de um único fonte de calor no trabalho. É possível fazer um órgão alto, mas não é possível fazer um órgão permanente)
Supondo que haja café quente na sala, há uma probabilidade muito alta de que o café esfrie aumentando a temperatura na sala. A condição em que o café está frio é expressa como alta entropia porque a probabilidade de ocorrência é alta, mas a condição em que o café não está resfriado é explicada pela baixa entropia. Assim, a entropia é uma lei que afirma que a entropia é um fator que é governado pela probabilidade. Além disso, todos os fenômenos vão na direção do aumento da entropia e, portanto, a entropia aumenta, e o café que já esfriou não pode ser aquecido novamente sozinho. Boltzmann entendeu o fenômeno do calor do ponto de vista estatístico e, como resultado, foi criado um novo campo chamado mecânica estatística.
* Observe que o texto acima é baseado no diagrama do livro do professor Ian Stewart “17 Equations That Changed the World”.
(54)

“Pensador. Aspirante a amante do Twitter. Empreendedor. Fã de comida. Comunicador total. Especialista em café. Evangelista da web. Fanático por viagens. Jogador.”
